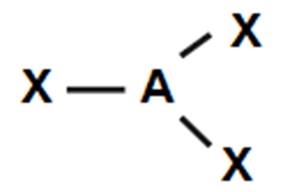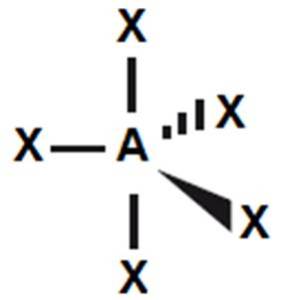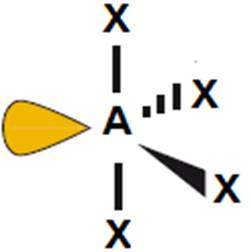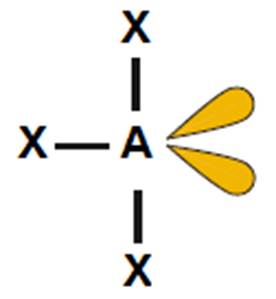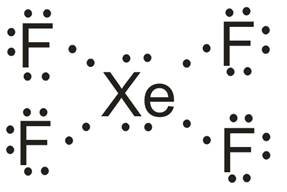Artykuł opublikowany w czasopiśmie Niedziałki w 2012 roku. Udostępniono za zgodą redakcji czasopisma.

Agnieszka Zaraska, Paweł Bernard Niedziałki 3/2012, s. 53-61

Wstęp

Kształt cząsteczki w istotny sposób wpływa na jej właściwości fizyczne. Zgodnie z podstawą programową z 2009 r. uczniowie gimnazjum powinni być w stanie opisać jedynie budowę cząsteczki wody i na tej podstawie opisać jej właściwości [1]. Natomiast w programie nauczania chemii na IV etapie edukacyjnym poziom rozszerzony, już w wymaganiach ogólnych czytamy: „Uczeń …, dostrzega zależność pomiędzy budową substancji a jej właściwościami fizycznymi i chemicznymi…”. W tym kontekście kluczowa wydaje się umiejętność określania kształtu cząsteczki, jednak niestety w podstawie programowej nie ujęto żadnej metody pozwalającej wyznaczyć kształty molekuł. W związku z tym, umiejętność zapisu wzorów strukturalnych nawet prostych molekuł jest związana z nauką pamięciową, a nie zrozumieniem tematu. Często określanie kształtu cząsteczek kojarzone jest z obliczeniami kwantowo-chemicznymi. Związane jest to z formą przedstawiania teorii dotyczącej określania kształtu cząsteczki w polskich podręcznikach. Teoria VSEPR (ang. Valence Shell Electron Pair Repulsion) pozwalająca określić kształt cząsteczki, zazwyczaj omawiana jest przy okazji przedstawiania teorii wiązań walencyjnych dla cząsteczek wieloatomowych w oparciu o orbitale zhybrydyzowane [2 – 6].

Teoria VSEPR a wyznaczanie typu hybrydyzacji

Najczęściej teoria VESPR jest utożsamiana ze wzorem pozwalającym wyliczyć liczbę orbitali zhybrydyzowanych i na tej podstawie wyznaczyć typ hybrydyzacji:

LH = σPW + WPE (1), [2]

gdzie:

LH – liczba hybryd (liczba orbitali zhybrydyzowanych),
σPW – liczba par elektronowych tworzących wiązanie (np. dla cząsteczki AB_x, σPW = 2),
WPE – liczba wolnych par elektronowych atomu centralnego, może być wyznaczona na podstawie wzoru Lewisa, lub:

WPE = ½ (a – x ∙ b) (2)

gdzie:

x – liczba atomów B w cząsteczce związku,
a – liczba elektronów walencyjnych atomu centralnego A,
b – liczba brakujących elektronów atomowi B do spełnienia reguły dubletu lub oktetu.

Na podstawie liczby hybryd określany jest typ hybrydyzacji. Do typu hybrydyzacji przypisuje się kształt figur geometrycznych, na których opisuje się rozkład orbitali. Uwzględniając liczbę wolnych par elektronowych określa się kształt cząsteczki. Przykładowo:

• dla metanu:

LH = 4 + ½ (4 – 4 ∙ 1) = 4 – hybrydyzacja sp³, brak wolnych par elektronowych – kształt cząsteczki: tetraedr.

• dla amoniaku:

LH = 3 + ½ (5 – 3 ∙ 1) = 4 – hybrydyzacja sp³, jedna wolna para elektronowa – kształt cząsteczki: piramida trygonalna.

Niestety teoria wiązań walencyjnych wraz z hybrydyzacją orbitali atomowych nie tłumaczą rozbieżności w kątach między wiązaniami dla cząsteczek opisanych na tej samej figurze geometrycznej, np.: metan: 109,5^o, amoniak 107^o. W tym miejscu autorzy zazwyczaj odwołują się do teorii VSEPR i w oparciu o niektórej z jej założeń tłumaczą wspomniane różnice. Tymczasem, teoria VSEPR jest teorią niezależną.

Wyznaczanie kształtu cząsteczki w oparciu o teorię VSEPR

Teoria VSEPR została opracowana w 1940 roku przez N.V. Sidgwicka i H.M. Powella [7], a jej rozwinięciem zajął się Ronald J. Gillespie [8, 9]. Teoria w ujęciu szkolnym może być przedstawiona w oparciu o trzy założenia:

• pary elektronowe są traktowane, jako obszary o wysokiej gęstości elektronowej i są tak rozmieszczone wokół atomu centralnego, aby siły odpychania między parami były jak najmniejsze,
• efekt odpychania dla niewiążących par elektronowych jest silniejszy niż dla par wiążących i zmienia się w kolejności:

para niewiążąca – para niewiążąca > para niewiążąca – para wiążąca > para wiążąca – para wiążąca

• wiązania wielokrotne traktowane są jak jeden obszar o wysokiej gęstości elektronowej, a jego oddziaływanie może być traktowane tak, jak oddziaływanie wiązań pojedynczych [10]. W bardziej szczegółowych opracowaniach, oddziaływanie wiązań wielokrotnych jest uznawane za większe niż wiązań pojedynczych, a mniejsze niż wolnych par elektronowych [8].

Teoria VSEPR w ujęciu szkolnym może posłużyć do opisu cząsteczek, w których atom centralny jest pierwiastkiem bloku s lub p. W oparciu o wzór elektronowy, którego umiejętność tworzenia jest jednym z obowiązkowych elementów wedle obowiązującej podstawy programowej, uczniowie mogą wyznaczyć:

• liczbę i krotność wiązań,
• liczbę wolnych par elektronowych.

Suma liczby wiązań i wolnych par elektronowych, czyli suma obszarów o wysokiej gęstości elektronowej, determinują figurę geometryczną, na której opisany jest kształt cząsteczki. Przyjmuje się, że atom centralny znajduje się w centrum figury, a obszary w których znajdują się pary elektronowe skierowane są w naroża. W tabeli nr 1 przedstawiono zestawienie kształtów oraz kątów między wiązaniami. Podane wartości są prawdziwe jedynie dla związków, w których wstępują tylko oddziaływania typu: para wiążąca – para wiążąca.

Tabela nr 1. Kształty oraz kąty między wiązaniami dla prostych cząsteczek [11].

Liczba obszarów o wysokiej gęstości elektronowej	Figura geometryczna	Kształt	Kąt między wiązaniami [o]
2	linia		180
3	trójkąt		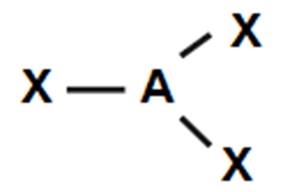120
4	tetraedr		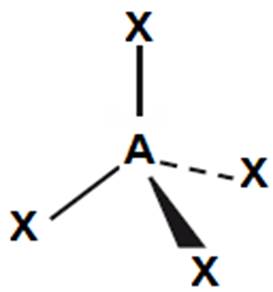109,5
5	bipiramida trygonalna		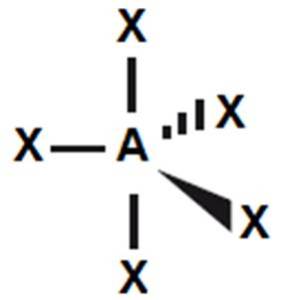120 i 90
6	oktaedr		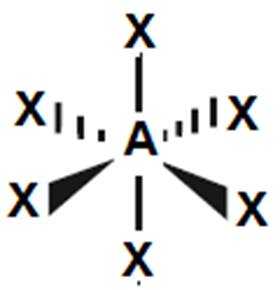90

O kształcie cząsteczki decyduje również liczba niewiążących par elektronowych. Ponieważ oddziaływanie z niewiążącą parą elektronową jest silniejsze, kąty pomiędzy wiązaniami sąsiadującymi z wolną parą elektronową ulegają zmniejszeniu. W przypadku sąsiadujących kilku par niewiążących efekt ten ulega zwiększeniu. Najczęściej spotykane kształty przedstawiono w tabeli nr 2.

Tabela nr 2. Kształty i kąty cząsteczek z uwzględnieniem wolnych par elektronowych [11].

Liczba obszarów o wysokiej gęstości elektronowej	Ilość		Rozmieszczenie par elektronowych (przykłady)	Przewidywany kształt cząsteczki lub jonu (kąt między wiązaniami)
	wiązań	wolnych par elektronowych
2	2	0	CO2, BeCl2	liniowy (180o)
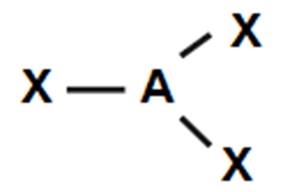
3	3	0	SO3, NO3–, BF3	trójkąt płaski (120o)
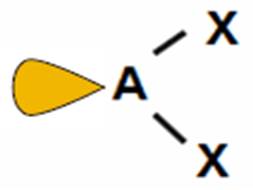
3	2	1	SO2, O3	cząsteczka kątowa (<120o)
4	4	0	CH4, H2SO4, ClO4−, NH4+	tetraedr (109,5o)
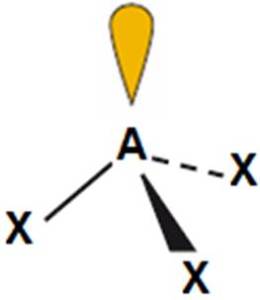
4	3	1	H3O+, NH3, PH3	piramida trygonalna (<109,5o)
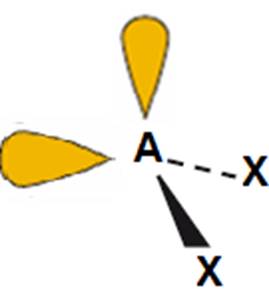
4	2	2	H2O, OF2, H2S	kątowy (<109,5o – mniejszy niż w przypadku jednej pary niewiążącej)
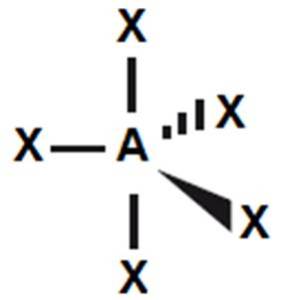
5	5	0	PF5	bipiramida trygonalna (120o i 90o)
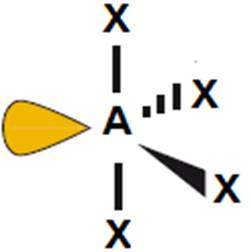
5	4	1	SF4	nieregularny tetraedr (<120o i <90o)
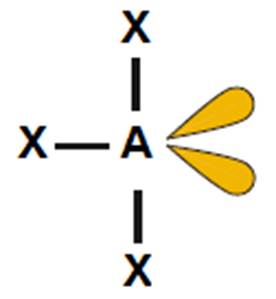
5	3	2	ClF3, BrF3	kształt litery T (<120o i <90o)
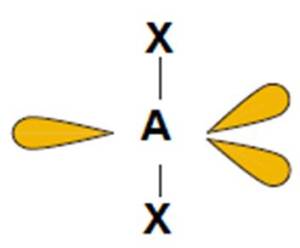
5	2	3	XeF2, I3−	liniowy (180o)
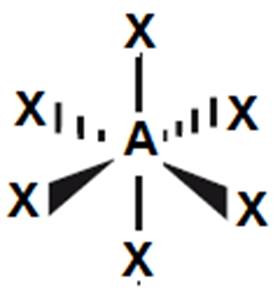
6	6	0	SF6	oktaedr (90o)
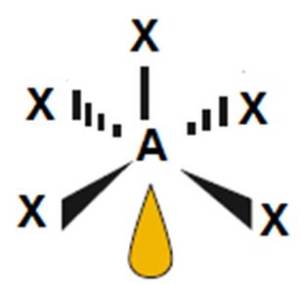
6	5	1	ClF5, BrF5	piramida kwadratowa (<90o)
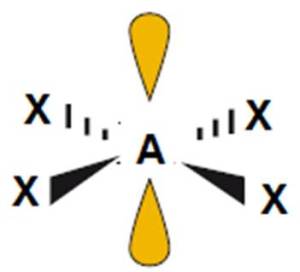
6	4	2	XeF4	kwadrat płaski (90o)

Poniżej przedstawiono kilka przykładów, pozwalających w prosty sposób określić kształt cząsteczki (jonu) oraz przybliżony kąt między wiązaniami.

A) Cząsteczka HCOOH

1. Atomem centralny w cząsteczce jest atom węgla (C).
2. Wzór elektronowy:
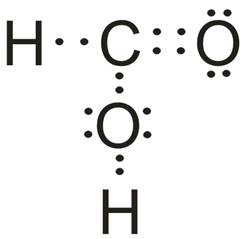
3. Liczba obszarów o wysokiej gęstości elektronowej: 3
4. Cząsteczka opisana jest na trójkącie równobocznym, kąt między wiązaniami: 120^o
5. Ze względu na brak niewiążących par elektronowych na atomie centralnym, cząsteczka HCOOH może być opisana jako trójkąt równoboczny.
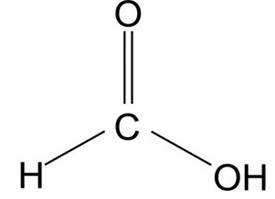
6. Jeśli uwzględnimy obecność wiązania wielokrotnego i związany z nim większy efekt odpychania, możemy stwierdzić, że kąt między wiązaniami jest inny niż 120^o, a cząsteczka nie jest idealnym trójkątem równobocznym.

B) Jon HCOO^–

1. Atomem centralny w cząsteczce jest atom węgla (C).
2. Wzór elektronowy:
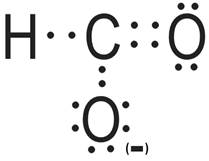
3. Liczba obszarów o wysokiej gęstości elektronowej: 3 – kształt jonu opisany na trójkącie równobocznym.
4. W jonie występuje delokalizacja wiązania π:
5. Jeśli nie uwzględnimy większego odpychania związanego z obecnością wiązania π jon HCOO^– można opisać jako trójkąt równoboczny (kąt między wiązaniami: 120^o).
6. Jeśli uwzględnimy obecność zdelokalizowanego wiązania π, możemy stwierdzić, że kąt między wiązaniami jest inny niż 120^o, a jon ma inny kształt niż opisana powyżej cząsteczka HCOOH.

C) Cząsteczka XeF₄

1. Atomem centralny w cząsteczce jest atom ksenonu (Xe).
2. Wzór elektronowy (Uwaga, w przypadku tej cząsteczki nie obowiązuje reguła oktetu):
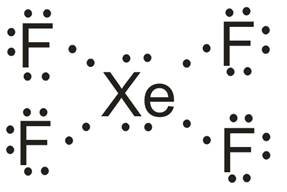
3. Liczba obszarów o wysokiej gęstości elektronowej: 6 – cząsteczka opisana na oktaedrze (kąty między wiązaniami: 90^o).
4. Wzór elektronowy wskazuje na obecność dwóch niewiążących par elektronowych na atomie centralnym. Odczytany z tabeli 2 kształt cząsteczki: kwadrat płaski.
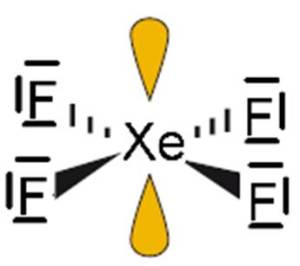
5. Niewiążące pary elektronowe rozmieszczone są symetrycznie. Z tego powodu ich obecność nie ma wpływu na kąt między wiązaniami.

D) Jon I₃^–

1. Atomem centralny w cząsteczce jest atom jodu (I).
2. Wzór elektronowy (Uwaga, w przypadku tej cząsteczki nie obowiązuje reguła oktetu):
3. Liczba obszarów o wysokiej gęstości elektronowej: 5 – jon opisany na bipiramidzie trygonalnej (kąty między wiązaniami: 90^o i 120^o).
4. Wzór elektronowy wskazuje na obecność trzech niewiążących par elektronowych na atomie centralnym. Odczytany z tabeli 2 kształt: cząsteczka liniowa.
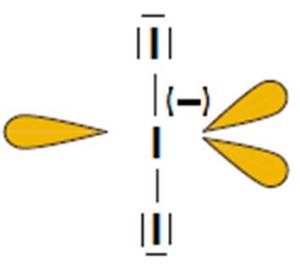
5. Podobnie jak w cząsteczce XeF₄ niewiążące pary elektronowe rozmieszczone są symetrycznie. Z tego powodu ich obecność nie ma wpływu na kąt między wiązaniami.

E) Cząsteczka NH₃

1. Atomem centralny w cząsteczce jest atom azotu (N).
2. Wzór elektronowy:
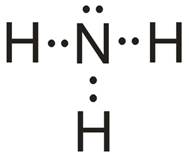
3. Liczba obszarów o wysokiej gęstości elektronowej: 4 – cząsteczka opisana na tetraedrze (kąty między wiązaniami: 109,5^o).
4. Wzór elektronowy wskazuje na obecność jednej niewiążącej pary elektronowej na atomie centralnym. Odczytany z tabeli 2 kształt cząsteczki: piramida trygonalna.
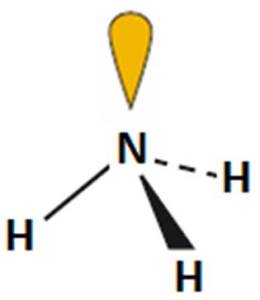
5. Obecność niewiążącej pary elektronowej na atomie centralnym powoduje zmniejszenie kąta między wiązaniami i deformację tetraedru (kąty ~ 107^o).

Podsumowanie

W ujęciu szkolnym teoria VSEPR opiera się o trzy proste założenia, wzory elektronowe i tabele kształtów cząsteczek. Zrozumienie teorii i umiejętność przewidywania kształtów cząsteczek oraz kątów między wiązaniami nie powinna nastręczać uczniom szkół ponadgimnazjalnych większych trudności. Na tej podstawie uczniowie mogą wnioskować o polarności cząsteczki, rodzajach oddziaływań międzycząsteczkowych i właściwościach fizyczny substancji.

Należy jednak pamiętać, że przedstawione ujęcie jest znacznym uproszczeniem. Odpychanie pomiędzy obszarami o wysokiej gęstości elektronowej może być omyłkowo utożsamiane jedynie z oddziaływaniem elektrostatycznym. W tym wypadku bardziej dociekliwi uczniowie mogą zapytać, dlaczego pary elektronowe odpychają się wzajemnie, a elektrony będące w parze, posiadające przecież taki sam ładunek, nie. Fakt ten może być wytłumaczony na podstawie zakazu Pauliego i spinów elektronów. Również z tego powodu traktowanie wiązań wielokrotnych, jako jednego obszaru o jednolitej gęstości elektronowej jest daleko idącym uproszczeniem. Czytelników zainteresowanych tymi problemami odsyłamy do bardziej szczegółowej literatury [8,9].

Literatura

[1] Rozporządzenie Ministra Edukacji Narodowej z dnia 23 grudnia 2008 r. w sprawie podstawy programowej wychowania przedszkolnego oraz kształcenia ogólnego w poszczególnych typach szkół Dzienniku Ustaw z dnia 15 stycznia 2009 r. Nr 4, poz. 17.
[2] M. M. Poźniczek, Zofia Kluz, Wybieram Chemię, ZamKor, Kraków 2008.
[3] R. Hass, A. Mrzigod, J. Mrzigod, W. Sułkowski, Chemia, Nowa Era, Gdańsk 2008.
[4] A. Czerwiński, A. Czerwińska, M. Kamińska, Chemia, WSiP, Warszawa 2004.
[5] B. Kałuża, F. Kamińska, Chemia ogólna i nieorganiczna, Wydawnictwo Edukacyjne Zofii Dobkowskiej, Warszawa 2003.
[6] K. M. Pazdro, W. Danikiewicz, Chemia, Oficyna Edukacyjna Krzysztof Pazdro, Warszawa 2009.
[7] N. V. Sidgwick, H. M. Powell, Stereochemical Types and Valency Groups, Proc. Roy. Soc. A, 176, 153-180 (1940).
[8] R. Gillespie, J. Chem. Educ. 81, 298, 2004.
[9] R. Gillespie, I. Hartgittai, The VSEPR Model of Molecular Geometry, Allyn and Bacon: Boston 1991.
[10] L. Jones, P. Atkins, Chemia ogólna cząsteczki, materia, reakcje. PWN, Warszawa 2006.
[11] J. Green, S. Damji, Chemistry 3^rd ed., IBID Press 2007.