Artykuł opublikowany w czasopiśmie Niedziałki w 2010 roku. Udostępniono za zgodą redakcji czasopisma. Treść poprawiona i dostosowana do publikacji na stronie internetowej.

Paweł Bernard, “Szkolny eksperyment ilościowy – termochemia, część I” Niedziałki 4/2010 s. 79-86

Eksperyment chemiczny stanowi nieodzowny element kształcenia chemicznego na każdym poziomie edukacji. Jak dotąd polska podstawa programowa z chemii zarówno na poziomie gimnazjalnym jak i ponadgimnazjalnym nie zobowiązuję uczących do przedstawiania eksperymentów ilościowych. Z tego powodu nauczyciele zapoznają uczniów jedynie z eksperymentami jakościowymi, a eksperyment ilościowy jest zazwyczaj opisywany tylko teoretycznie. Trendy światowe są w tej kwestii całkowicie odmienne. Uczniowie zdający maturę międzynarodową, nie tylko są zapoznawani z metodologią eksperymentów ilościowych, ale są zobowiązani samodzielnie takie eksperymenty wykonywać podczas zajęć lekcyjnych.

W polskich programach nauczania chemiczne eksperymenty ilościowe pojawiają się sporadycznie. Jednym z takich eksperymentów jest proponowany pomiar ilości tlenu w powietrzu przez nakrycie świeczki pływającej na powierzchni wody zlewką i zmierzenie, na jaki poziom podniesie się woda. Eksperyment ten, mimo iż często daje prawidłowy wynik, budzi wiele kontrowersji. Przykładowo jak zachowa się układ, gdy zamiast jednej wprowadzimy 2 świeczki? W programie nauczania szkół ponadgimnazjalnych uczniowie mogą spotkać się z opisem techniki miareczkowania, ale nawet w tym przypadku nieczęsto nauczyciele przedstawiają tę technikę w formie pokazu, nie wspominając o samodzielnej pracy ucznia.

Dzisiejsza chemia opiera się na eksperymentach ilościowych, tymczasem na lekcjach chemii odtwarzane są doświadczenia jakościowe z XVIII – XIX wieku. Oczywiście pozwalają one kształtować umiejętności prowadzenia obserwacji i wyciągania wniosków, jednak brak eksperymentów ilościowych skutkuje tym, iż uczniowie otrzymują mylny wizerunek chemii jako nauki jak i pracy chemików zarówno w laboratoriach przemysłowych jak i naukowych. Uczniowie nie spotykają się z problemami analizy wyników liczbowych, typami i analizą błędów pomiarowych czy programami do analizy graficznej i statystycznej.

Brak eksperymentów o charakterze ilościowym jest zazwyczaj tłumaczony znacznymi kosztami urządzań pomiarowych i czasochłonnością tych eksperymentów. Tymczasem okazuje się, że odrobina kreatywności pozwala prowadzić eksperymenty ilościowe nawet w pracowni szkolnej wyposażonej w podstawowy sprzęt laboratoryjny. Poniżej przedstawiono kilka doświadczeń fizyko-chemicznych, które nie wymagają wyszukanego sprzętu, pozwalają jednak zapoznać uczniów z podstawami eksperymentów ilościowych. W tym artykule przedstawione zostaną eksperymenty obrazujące prawa i zależności z działu „Termochemia”. Doświadczenia te mogą być przedstawione przez nauczyciela w postaci pokazu, lub wykonane samodzielnie przez uczniów podczas lekcji lub zajęć koła chemicznego.

UWAGA: Przedstawione przepisy i wyniki zostały opracowane i uzyskane przez uczniów podczas zajęć lekcyjnych pod nadzorem autora. Przedstawione w przepisach wartości liczbowe (stężenia itd.) mogą, a nawet powinny być modyfikowane. Przedstawione wartości końcowe stanowią jedynie przykład, nie należy traktować ich w sposób ścisły lub jako wartości odniesienia.

Doświadczenia nr 1: Wyznaczanie rzeczywistego składu soli udowodnionej.

Odczynniki: CuSO₄∙5H₂O

Sprzęt: tygiel, szczypce, palnik, statyw z trójkątem ceramicznym dopasowanym do tygla, waga.

Opis wykonania: Należy wyznaczyć masę tygla wraz z pokrywką, (tygiel można wyprażyć przed ważeniem). Następnie tygiel wypełnić do około 1/3 objętości próbką soli (CuSO₄∙xH₂O) i zważyć. Próbkę należy wyprażyć do stałej masy, pierwsze prażenie może być dłuższe niż pozostałe np.: 10 min, kolejne po 5 min. Po każdym prażeniu należy poczekać aż tygiel ostygnie i zważyć. Zazwyczaj zmiany masy po 4 i 5 prażeniu są zaniedbywalnie małe.

Przykładowe wyniki

Tabela nr 1. Przykładowe wyniki otrzymane podczas rozkładu próbki soli CuSO₄∙xH₂O

	Masa tygla z próbką [g] (±0,005 g)	Masa próbki [g] (±0,01 g)	Zmiana masy próbki [g] (±0,02 g)
Przed prażeniem	43,26	29,20	–
Po prażeniu nr 1	36,51	22,45	-6,75
Po prażeniu nr 2	34,07	20,01	-2,44
Po prażeniu nr 3	32,54	18,48	-1,53
Po prażeniu nr 4	32,47	18,41	-0,07

Masa molowa soli bezwodnej: M_CuSO4 = 159,6 g/mol

Stosunek masowy: CuSO₄ do H₂O → 18,41 do 10,79 g

Obliczony empiryczny stosunek molowy CuSO₄ do H₂O 0,115 do 0,599

W przeliczeniu na 1 mol CuSO₄ → 1:5,21

Wzór rzeczywisty soli: CuSO₄ ∙ 5,21H₂O

Doświadczenie nr 2: Wyznaczanie temperatury krzepnięcia naftalenu.

Odczynniki: naftalen.

Sprzęt: termometr, statyw z łapą do probówek, probówka, zlewka, elektryczna płyta grzewcza lub mieszadło magnetyczne z funkcją grzania.

Opis wykonania: Probówkę do 2/3 wysokości wypełniamy naftalenem i wprowadzamy termometr. Następnie probówkę umieszczamy w łaźni wodnej. Łaźnię wodną może stanowić zlewka z gorąca wodą umieszczoną na elektrycznej płycie grzewczej. Czekamy aż cały naftalen ulegnie stopieniu. Gdy temperatura w probówce osiągnie około 90 stopni usuwamy zlewkę z gorącą wodą. Zapisujemy wskazania termometru w jednakowych odstępach czasu. (Wygląd krzywej topnienia będzie bardziej poglądowy, gdy umieścimy probówkę w chłodnym miejscu lub zlewce wypełnionej wodą o temp. około 50 °C).

Uwaga! Nie należy ogrzewać probówki z naftalenem w płomieniu palnika, ciekły naftalen jest łatwopalny!

Przykładowe wyniki: Pomiar temperatury prowadzony był w 10 sekundowych odstępach czasu. Zebrane wyniki zostały naniesione na wykres zależności temperatury od czasu (wykres nr 1).

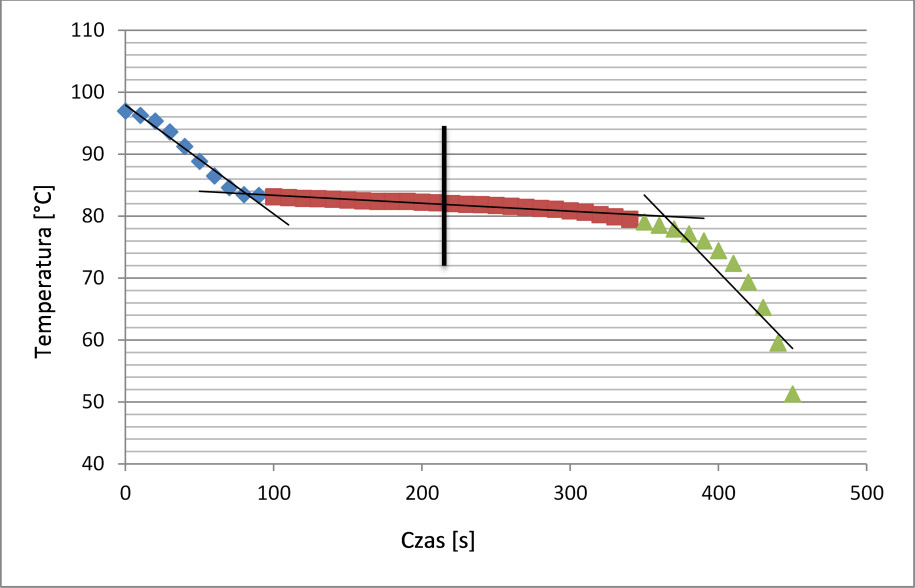
Wykres 1. Zmiany temperatury podczas chłodzenia naftalenu.

Dane na wykresie podzielono na 3 serie do których dopasowano linie proste. Dwie serie są związane z dużym gradientem temperatury, a jedna z zakresem małych zmian. Jako temperaturę topnienia (krzepnięcia) można przyjąć temperaturę w połowie długości linii trendu dopasowanej do serii danych o niewielkiej zmienności temperatur.

Wyznaczona temperatura topnienia naftalenu: 81 °C

Doświadczenie nr 3: Efekt energetyczny reakcji Zn z Cu²⁺.

Odczynniki: CuSO₄­, Zn (proszek).

Sprzęt: termometr, waga, styropianowe kubki do kawy, mieszadło magnetyczne (opcjonalnie).

Przykładowy opis wykonania: W doświadczeniu uczniowie badają efekt energetyczny towarzyszący reakcji wypierania miedzi z roztworu przez bardziej aktywny metal.

Zn_(s) + Cu²⁺_(aq) = Zn²⁺_(aq) + Cu_(s)

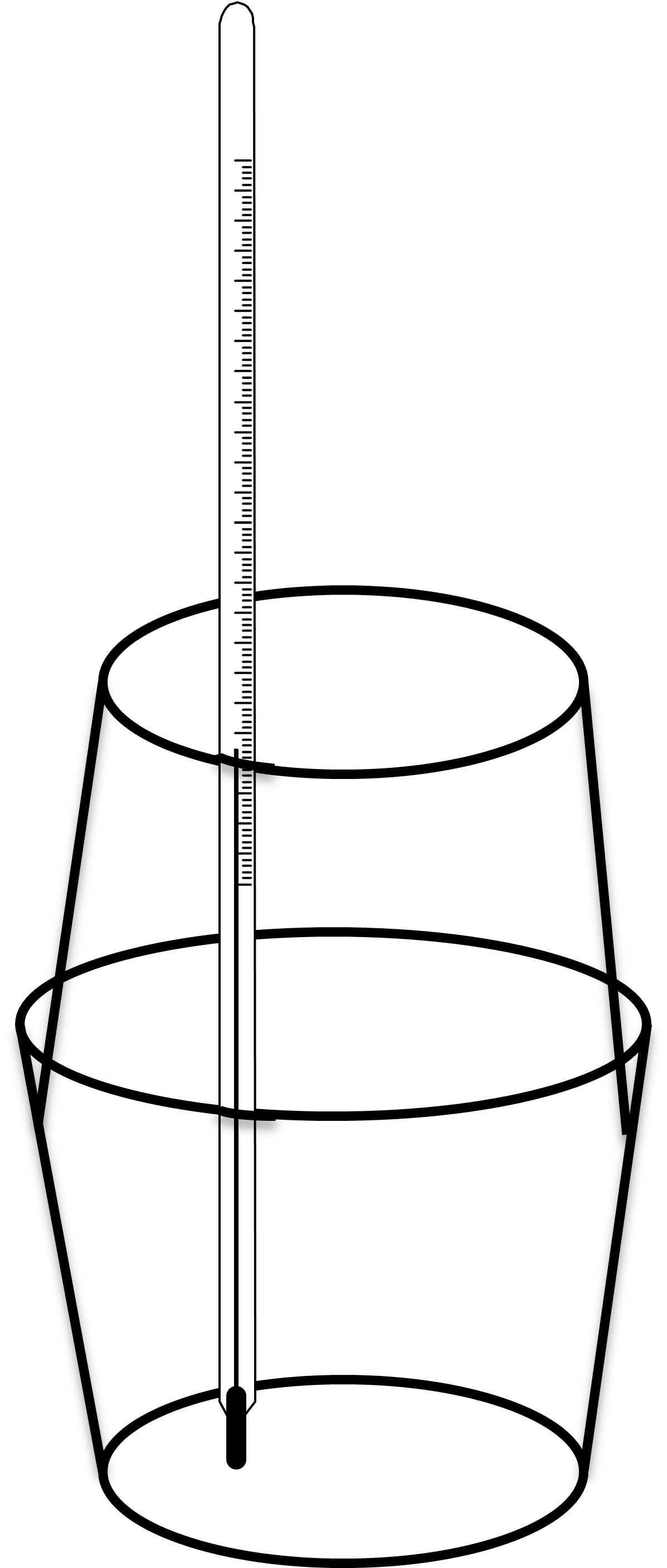
Doświadczenie opiera się na pomiarze temperatury, zatem powinno być przeprowadzone w kalorymetrze. Prosty kalorymetr można wykonać z dwóch kubków styropianowych do kawy. Jeden kubek stanowi naczynie, w którym prowadzimy reakcję, drugi należy obciąć w 2/3 wysokości, będzie on pokrywką kalorymetru. W pokrywce należy wykonać otwór, przez który wprowadzany jest termometr do naczynia (Rysunek nr 1). W naczyniu umieszczamy 25,0 cm³ roztworu soli miedzi o stężeniu 1 mol/dm³ i mierzymy temperaturę. Następnie wsypujemy około 5 g pyłu Zn. Cynk jest w nadmiarze (należy zwrócić uwagę, że zbyt duży nadmiar cynku może wpłynąć na wyniki, ze względu na dużą pojemność cieplną metalu). Zamykamy kalorymetr i mierzymy temperaturę w przyjętych wcześniej odstępach czasu. Roztwór należy mieszać poruszając całym naczyniem, lub wykorzystać mieszadło magnetyczne.

Rysunek 1. Schemat kalorymetru, w którym można przeprowadzić reakcję Zn_(s) + Cu²⁺_(aq)

Przykładowe wyniki przedstawiono na wykresie 2.

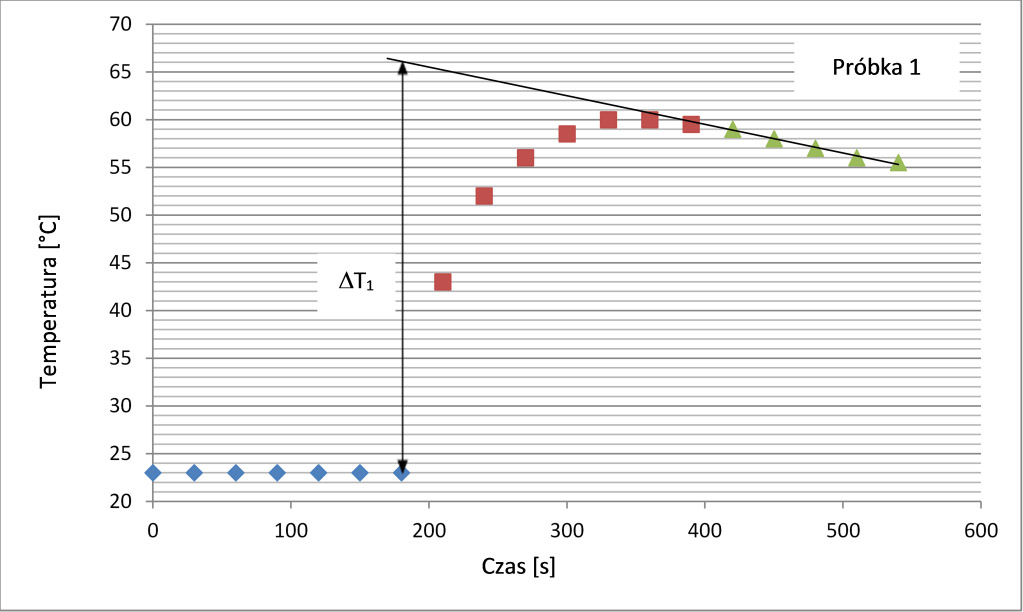
Wykres 2. Zależność temperatury względem czasu dla reakcji Zn_(s) + Cu²⁺_(aq); próbka 1.

Przyrost temperatury można wyznaczyć, jako różnicę miedzy temperaturą początkową, a temperaturą maksymalną. Jednak wartości bardziej zbliżone do literaturowych pozwala otrzymać graficzna analiza wyników, analogiczna do przedstawionej na wykresie 2. W tym przypadku zakres danych otrzymanych bezpośrednio po uzyskaniu temperatury maksymalnej potraktowano, jako osobną serie danych. Do tej serii dopasowano prostą, która została ekstrapolowana do czasu pierwszego przyrostu temperatury. Zmianę temperatury podczas procesu wyznaczono jako różnicę między temperaturą początkową, a temperaturą wskazaną przez dopasowaną prostą. Metodę tę stosuje się gdy zmiana temperatury następuje w sposób gwałtowny, a co za tym idzie początkowo pojawiają się znaczne straty ciepła (duża ilość ciepła jest absorbowana przez kalorymetr i emitowana do otoczenia). Zabieg ten przynajmniej częściowo rekompensuje początkowe straty cieplne.

Entalpię reakcji obliczamy na podstawie równania:

Q = m · c · ∆T (1)

gdzie:

m – masa wody (r-ru),
c – pojemność cieplna wody (4,18 [J∙K^-1g^-1]),
∆T – wyznaczona zmiana temperatury.

Można założyć, że gęstość roztworu wynosi 1 g/cm³.

Ilość ciepła pobrana przez wodę:

Q = 25,0 · 4,18 · 40,5 = 4,23 kJ

Ciepło pobrane przez wodę zostało wydzielone w trakcie reakcji. Zatem zmiana entalpii w trakcie reakcji wynosi:

∆H = -Q (2)

W doświadczeniu użyto nadmiaru cynku, zatem efekt energetyczny można odnieść do ilości moli jonów miedzi w roztworze. Użyto 25,0 cm³ roztworu o stężeniu 1 mol/dm³, więc liczba moli Cu²⁺ w roztworze wynosiła 0,025 mola. Po przeliczeniu na 1 mol:

∆H = -169,3 kJ/mol

Doświadczenie nr 4: Wyznaczenie entalpii reakcji hydratacji CuSO₄.

Wstęp: Celem doświadczenia jest wyznaczenie entalpii reakcji:

CuSO_4(s) + xH₂O = CuSO₄ ∙ xH₂O_(s)

Bezpośrednie wyznaczenie entalpii tej reakcji byłoby trudne do wykonania. Można jednak skorzystać z prawa Hessa i dojść do wyniku „inną drogą”. Skonstruowany cykl zmian entalpii przedstawiono na rysunku nr 2.

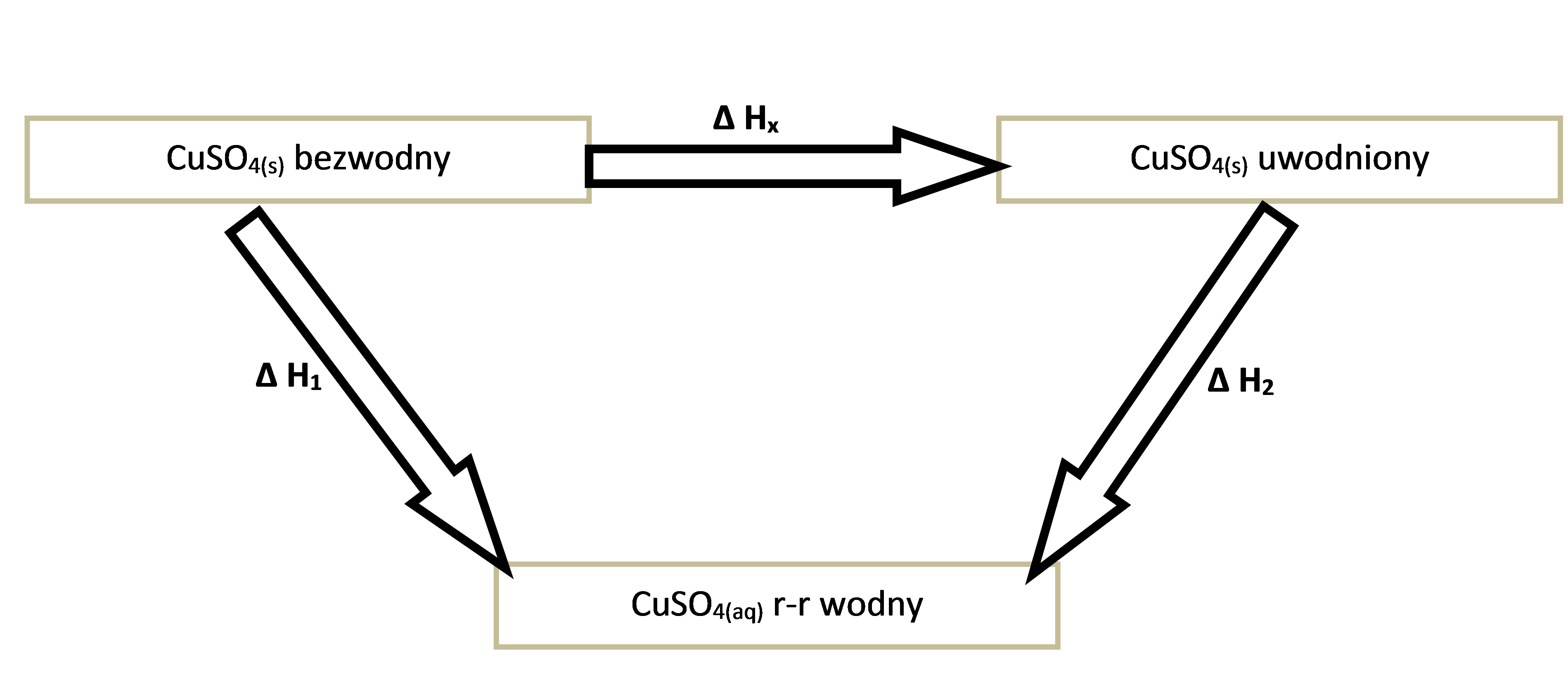
Rysunek 2. Cykl przemian pozwalający wyznaczyć entalpię reakcji hydratacji stałego siarczanu(VI) miedzi(II) w sposób niebezpośredni.

Na podstawie diagramu stwierdzamy, że entalpia szukanej reakcji może być obliczona, jako:

∆H_x = ∆H₁ + (-∆H₂ ) (3)

Odczynniki: CuSO₄ uwodniony, CuSO₄ bezwodny (można wyprażyć sól uwodnioną).

Sprzęt: termometr, waga, kubki do kawy styropianowe, mieszadło magnetyczne (opcjonalnie).

Przykładowy opis wykonania: Doświadczenie oparte jest na pomiarze efektu energetycznego towarzyszącego rozpuszczaniu soli uwodnionej i bezwodnej. Doświadczenie można wykonać w kalorymetrze opisanym w „Doświadczeniu nr 3”. W naczyniu kalorymetrycznym umieszczamy 100 g wody i mierzymy jej temperaturę. Następnie wsypujemy próbkę soli o znanej masie, około 5,5 – 6,0 g soli bezwodnej lub około 10 g soli uwodnionej. Próbkę mieszamy. Każdy z procesów należy przeprowadzać do otrzymania, co najmniej trzech zbieżnych wyników. W doświadczeniu można użyć sól bezwodną i wyznaczony stopień uwodnienia hydratu w „Doświadczeniu nr 1”.

Przykładowe wyniki

Tabela 2. Wyniki pomiaru zmian temperatury dla procesów rozpuszczania bezwodnego i uwodnionego siarczanu(VI) miedzi(II).

CuSO4 bezwodny
Próbka	Masa [g] (±0,005)	Temp wody [°C] (±0,05)	Tempmax r-ru [°C] (±0,05)	∆T [°C] (±0,1)
1	5,62	22,5	27,8	5,3
2	5,45	22,8	27,8	5,0
3	5,93	23,1	28,6	5,5
CuSO4 ∙ 5,21H2O
Próbka	Masa [g] (±0,005g)	Temp wody [°C] (±0,05)	Tempmax r-ru [°C] (±0,05)	∆T [°C] (±0,1)
1	9,81	23,1	22,1	-1,0
2	10,15	23,5	22,1	-1,4
3	10,04	23,1	22,1	-1,0

Zmianę entalpii obliczamy na podstawie równania nr 1 i 2. Na podstawie mas molowych obliczamy liczbę moli użytej substancji, a następnie przeliczamy efekt energetyczny na 1 mol (M_CuSO4 = 159,62 g/mol; M_{CuSO4∙5,21H2O} = 253,40 g/mol).

Proces rozpuszczania bezwodnego CuSO₄ obserwujemy wzrost temperatury, jest to zatem proces egzotermiczny, więc entalpia tego procesu powinna przyjmować wartości ujemne, natomiast proces rozpuszczania hydratu CuSO₄ jest endotermiczny, zatem zmiana entalpii musi być dodatnia.

Tabela 3. Obliczona entalpia procesów rozpuszczania bezwodnego i uwodnionego siarczanu(VI) miedzi(II).

Próbka		Masa [g] (±0,005g)	∆T [°C] (±0,1)	Q [J∙g-1]	Liczba moli soli	Q [J∙mol-1]	Średnia ∆H [kJ∙mol-1]
CuSO4 bezwodny	1	5,62	5,3	2199,5	0,035209	62470,5	-61,6
	2	5,45	5,0	2075,0	0,034144	60772,8
	3	5,93	5,5	2282,5	0,037151	61438,9
CuSO4 ∙ 5,21H2O	1	9,81	-1,0	-415,0	0,038713	-10719,8	11,9
	2	10,15	-1,4	-581,0	0,040055	-14505,0
	3	10,04	-1,0	-415,0	0,039621	-10474,2

Korzystając z równania 3 obliczamy zmianę entalpii podczas procesu hydratacji bezwodnego siarczanu(VI) miedzi(II):

∆H_x = ∆H₁ + (-∆H₂ ) = -73,5 kJ∙mol^-1

Jest to proces egzotermiczny.

Doświadczenie nr 5: Porównanie entalpii spalania wybranych alkoholi.

Wstęp: Eksperyment pozwala na wyznaczenie entalpii spalania alkoholi i innych paliw ciekłych. Ze względu na konieczność pomiaru ciepła reakcji i strat z tym związanych nie zaleca się poszukiwania konkretnej wartości dla danego paliwa, a porównanie kilku paliw i wyznaczanie trendu zmian, np. ze względu na wzrost długości łańcucha węglowego. Przebieg spalania alkoholi przedstawia ogólne równanie:

C_nH_2n+1OH + (3n/2)O₂ = nCO₂ + (n+1)H₂O (4)

Podobnie jak poprzednie eksperymenty doświadczenie to opiera się na pomiarze zmian temperatury. Również do tego pomiaru można skonstruować prosty kalorymetr.

Przykład budowy kalorymetru: Główną część kalorymetru można wykonać z pudełka po butach. W pudełku należy wyciąć dwa otwory: otwór przez który wprowadzane będzie ciepło płomienia palnika (rysunek nr 3, element nr 5), oraz drugi otwór tzw. „okienko” (rysunek nr 3, element nr 2) – otwór ten będzie służył do kontroli temperatury wewnątrz kalorymetru, w otwór należy wpasować i przykleić np.: połowę szalki Petriego. Ściany pudełka należy obłożyć folią aluminiową, poprawia to izolację oraz zabezpiecza kalorymetr przed zapaleniem.

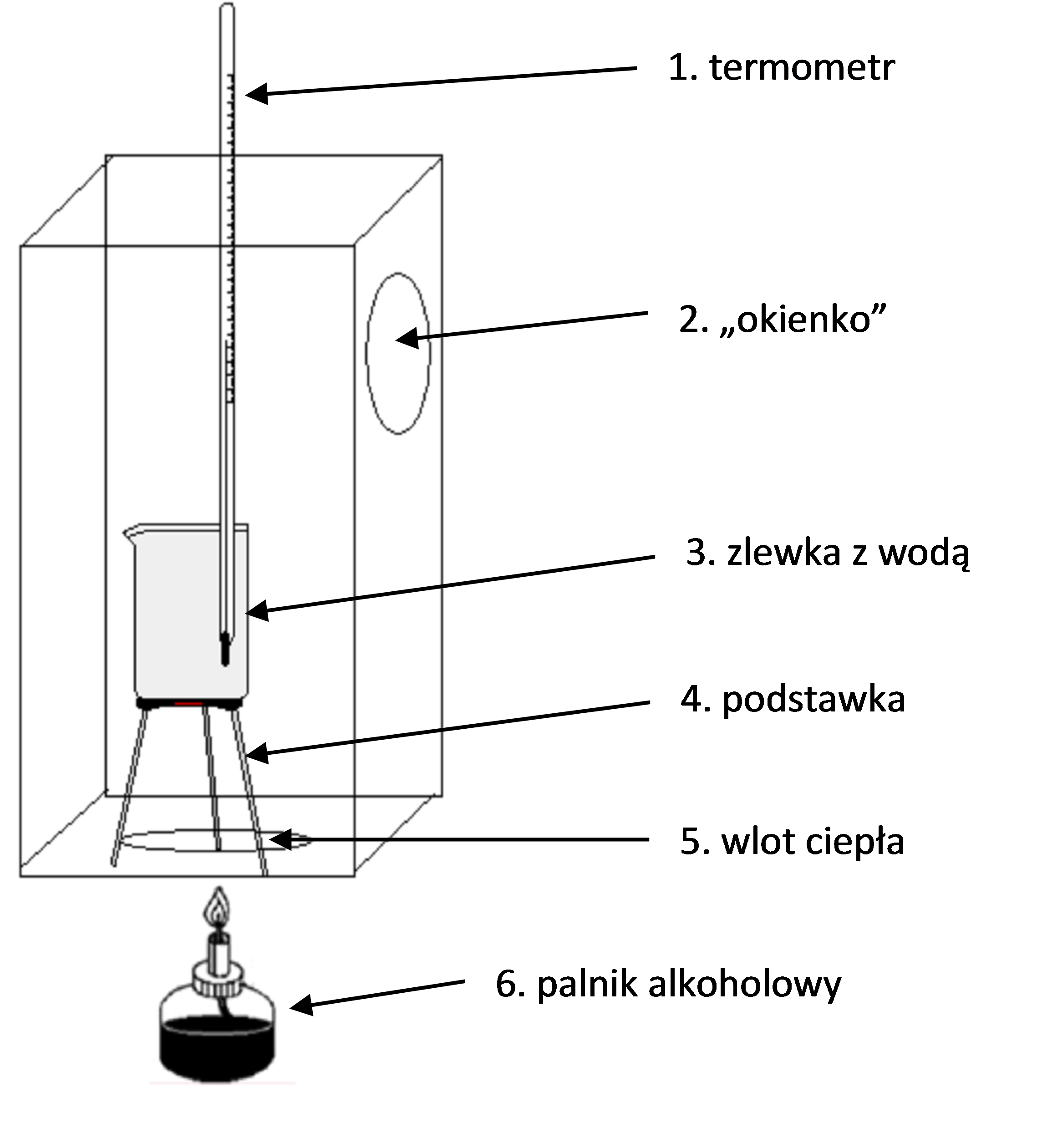
Rysunek 3. Schemat budowy kalorymetru do wyznaczania entalpii spalania paliw ciekłych.

Sprzęt: termometr, waga, palnik alkoholowy, kalorymetr (wykonany wg. rysunku nr 3)

Odczynniki: wybrane alkohole np.: etanol, propan-1-ol, butan-1-ol.

Przykładowy opis wykonania: W kalorymetrze umieszczamy zlewkę zawierającą 200 g wody i mierzymy jej temperaturę. Palnik wypełniamy badanym paliwa. Prowadzimy ogrzewanie do około 75 °C. Masę zużytego alkoholu należy wyznaczyć ważąc palnik z alkoholem przed i po ogrzewaniu. Odległość między płomieniem palnika a otworem w pudełku należy dopasować tak, aby nie zapalić pudełka i jednocześnie zminimalizować straty ciepła. Uzyskane wartości najpierw przeliczamy na 1 g, a następnie na 1 mol paliwa.

Przykładowe wyniki. W tabeli nr 4 zebrano opracowane wyniki pomiarów.

Tabela 4. Wyniki zmian temperatury związane z procesami spalania badanych alkoholi i wyznaczone na tej podstawie ciepło spalania.

Alkohol	Masa zużytego alkoholu [g] (±0,0015)	Masa wody [g] (±0,0005)	∆T [°C] (±2)	Ciepło spalania [J∙g-1]	Ciepło spalania [J∙mol-1]	Średnie ciepło spalania [kJ∙mol-1]
Etanol	2,452	200,213	55	18772	865390	903
	2,213	200,114	54	20411	940951
Propan-1-ol	1,924	200,323	55	23937	1438837	1486
	1,803	199,965	55	25497	1532653
Butan-1-ol	1,779	200,311	55	25886	1919201	1962
	1,705	200,529	55	27039	2004677

Na wykresie nr 3 można zaobserwować wzrost efektywności energetycznej paliw wraz ze wzrostem długości łańcucha węglowego.

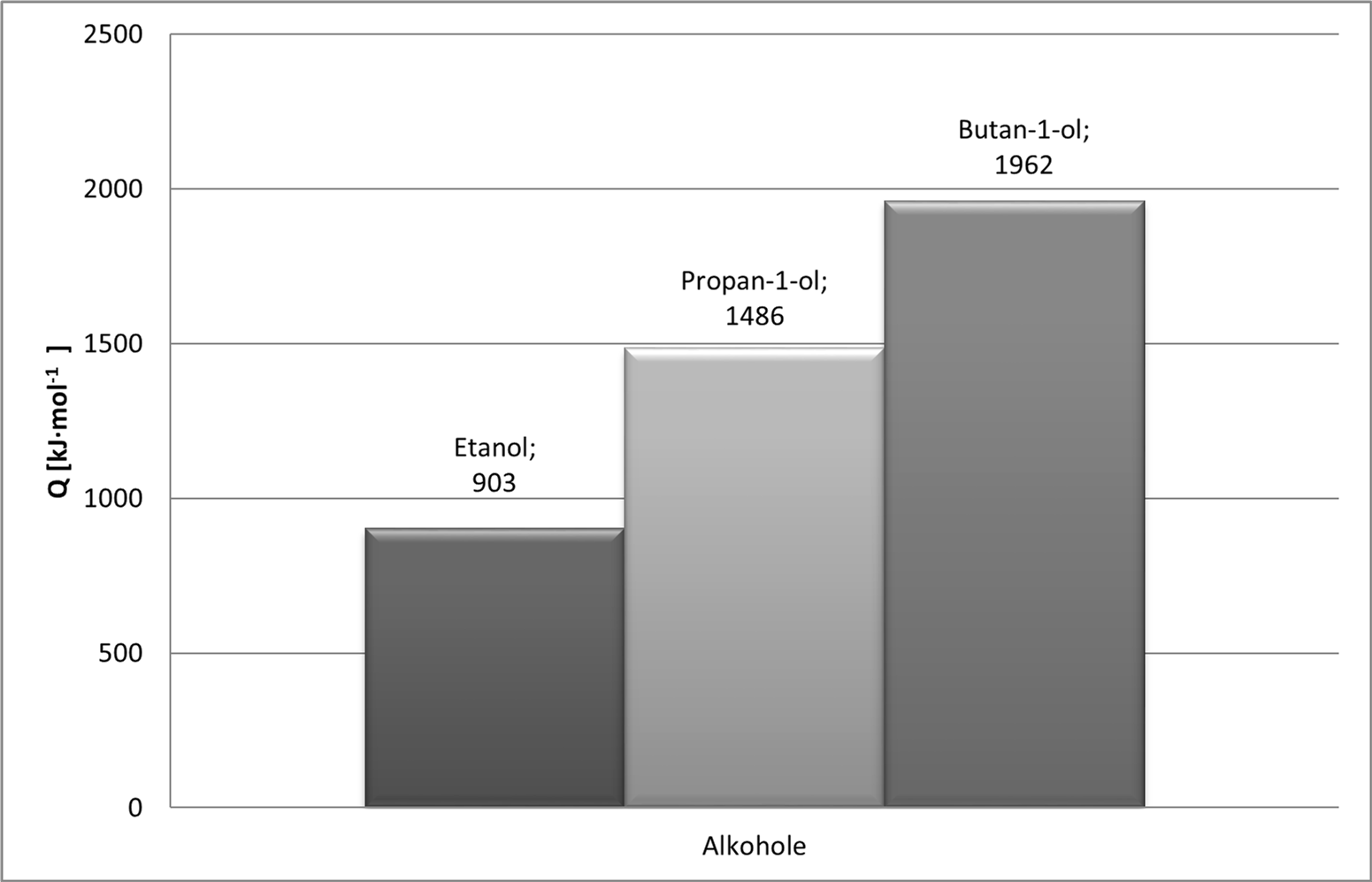
Wykres 3. Porównanie ciepła spalania wybranych alkoholi.

Podsumowanie

Przedstawione eksperymenty wykorzystują podstawowy sprzęt jakim jest termometr i waga laboratoryjna do pomiarów ilościowych. Eksperymenty te mogą być wykonywane samodzielnie przez uczniów. Ich wartość wzrośnie jeszcze bardziej, gdy nie podamy uczniom gotowego przepisu, a jedynie nakreślimy ideę pomiaru. Uczniowie samodzielnie powinni dopracować metodę, wybrać stężenia roztworów, ilości mieszanych cieczy oraz przygotować kalorymetry. Takie podejście jest zgodne z tak popularnym w ostatnim czasie nauczaniem przez odkrywanie (ang.: IBSE – Inquiry Based Science Education). Uczniowie mogą samodzielnie wybrać proces fizyczny lub chemiczny, którego efekt energetyczny chcieliby wyznaczyć, mogą do tego wykorzystać przedstawione techniki. Możemy pozwolić uczniom pobłądzić po świecie nauki, samemu zadać pytania i na nie odpowiedzieć. Dodatkowo daje nam to okazję wykazać dlaczego obliczenia chemiczne, których coraz to wyższe poziomy trudności uczniowie opanowują na kolejnych szczeblach edukacji, są tak istotne.

Literatura:

1. John Green, Sadru Damji Chemistry 3rd Edition Textbook, IBID Press, 2007
2. John Green, A Portfolio of Investigations for IB Chemistry, IBID Press, 2005
3. Geoffrey Neuss Chemistry for the IB Diploma 2E, Oxford University Press, 2007
4. Christopher Talbot Student Guide for Assessed Practical Work, IBID Press, 2006
5. Chemistry Data Booklet for the first examinations 2010, Antony Rowe Ltd, Chippenham, Wiltshire, 2007

Artykuł opublikowany w czasopiśmie Niedziałki w 2012 roku. Udostępniono za zgodą redakcji czasopisma.

Agnieszka Zaraska, Paweł Bernard Niedziałki 3/2012, s. 53-61

Wstęp

Kształt cząsteczki w istotny sposób wpływa na jej właściwości fizyczne. Zgodnie z podstawą programową z 2009 r. uczniowie gimnazjum powinni być w stanie opisać jedynie budowę cząsteczki wody i na tej podstawie opisać jej właściwości [1]. Natomiast w programie nauczania chemii na IV etapie edukacyjnym poziom rozszerzony, już w wymaganiach ogólnych czytamy: „Uczeń …, dostrzega zależność pomiędzy budową substancji a jej właściwościami fizycznymi i chemicznymi…”. W tym kontekście kluczowa wydaje się umiejętność określania kształtu cząsteczki, jednak niestety w podstawie programowej nie ujęto żadnej metody pozwalającej wyznaczyć kształty molekuł. W związku z tym, umiejętność zapisu wzorów strukturalnych nawet prostych molekuł jest związana z nauką pamięciową, a nie zrozumieniem tematu. Często określanie kształtu cząsteczek kojarzone jest z obliczeniami kwantowo-chemicznymi. Związane jest to z formą przedstawiania teorii dotyczącej określania kształtu cząsteczki w polskich podręcznikach. Teoria VSEPR (ang. Valence Shell Electron Pair Repulsion) pozwalająca określić kształt cząsteczki, zazwyczaj omawiana jest przy okazji przedstawiania teorii wiązań walencyjnych dla cząsteczek wieloatomowych w oparciu o orbitale zhybrydyzowane [2 – 6].

Teoria VSEPR a wyznaczanie typu hybrydyzacji

Najczęściej teoria VESPR jest utożsamiana ze wzorem pozwalającym wyliczyć liczbę orbitali zhybrydyzowanych i na tej podstawie wyznaczyć typ hybrydyzacji:

LH = σPW + WPE (1), [2]

gdzie:

LH – liczba hybryd (liczba orbitali zhybrydyzowanych),
σPW – liczba par elektronowych tworzących wiązanie (np. dla cząsteczki AB_x, σPW = 2),
WPE – liczba wolnych par elektronowych atomu centralnego, może być wyznaczona na podstawie wzoru Lewisa, lub:

WPE = ½ (a – x ∙ b) (2)

gdzie:

x – liczba atomów B w cząsteczce związku,
a – liczba elektronów walencyjnych atomu centralnego A,
b – liczba brakujących elektronów atomowi B do spełnienia reguły dubletu lub oktetu.

Na podstawie liczby hybryd określany jest typ hybrydyzacji. Do typu hybrydyzacji przypisuje się kształt figur geometrycznych, na których opisuje się rozkład orbitali. Uwzględniając liczbę wolnych par elektronowych określa się kształt cząsteczki. Przykładowo:

• dla metanu:

LH = 4 + ½ (4 – 4 ∙ 1) = 4 – hybrydyzacja sp³, brak wolnych par elektronowych – kształt cząsteczki: tetraedr.

• dla amoniaku:

LH = 3 + ½ (5 – 3 ∙ 1) = 4 – hybrydyzacja sp³, jedna wolna para elektronowa – kształt cząsteczki: piramida trygonalna.

Niestety teoria wiązań walencyjnych wraz z hybrydyzacją orbitali atomowych nie tłumaczą rozbieżności w kątach między wiązaniami dla cząsteczek opisanych na tej samej figurze geometrycznej, np.: metan: 109,5^o, amoniak 107^o. W tym miejscu autorzy zazwyczaj odwołują się do teorii VSEPR i w oparciu o niektórej z jej założeń tłumaczą wspomniane różnice. Tymczasem, teoria VSEPR jest teorią niezależną.

Wyznaczanie kształtu cząsteczki w oparciu o teorię VSEPR

Teoria VSEPR została opracowana w 1940 roku przez N.V. Sidgwicka i H.M. Powella [7], a jej rozwinięciem zajął się Ronald J. Gillespie [8, 9]. Teoria w ujęciu szkolnym może być przedstawiona w oparciu o trzy założenia:

• pary elektronowe są traktowane, jako obszary o wysokiej gęstości elektronowej i są tak rozmieszczone wokół atomu centralnego, aby siły odpychania między parami były jak najmniejsze,
• efekt odpychania dla niewiążących par elektronowych jest silniejszy niż dla par wiążących i zmienia się w kolejności:

para niewiążąca – para niewiążąca > para niewiążąca – para wiążąca > para wiążąca – para wiążąca

• wiązania wielokrotne traktowane są jak jeden obszar o wysokiej gęstości elektronowej, a jego oddziaływanie może być traktowane tak, jak oddziaływanie wiązań pojedynczych [10]. W bardziej szczegółowych opracowaniach, oddziaływanie wiązań wielokrotnych jest uznawane za większe niż wiązań pojedynczych, a mniejsze niż wolnych par elektronowych [8].

Teoria VSEPR w ujęciu szkolnym może posłużyć do opisu cząsteczek, w których atom centralny jest pierwiastkiem bloku s lub p. W oparciu o wzór elektronowy, którego umiejętność tworzenia jest jednym z obowiązkowych elementów wedle obowiązującej podstawy programowej, uczniowie mogą wyznaczyć:

• liczbę i krotność wiązań,
• liczbę wolnych par elektronowych.

Suma liczby wiązań i wolnych par elektronowych, czyli suma obszarów o wysokiej gęstości elektronowej, determinują figurę geometryczną, na której opisany jest kształt cząsteczki. Przyjmuje się, że atom centralny znajduje się w centrum figury, a obszary w których znajdują się pary elektronowe skierowane są w naroża. W tabeli nr 1 przedstawiono zestawienie kształtów oraz kątów między wiązaniami. Podane wartości są prawdziwe jedynie dla związków, w których wstępują tylko oddziaływania typu: para wiążąca – para wiążąca.

Tabela nr 1. Kształty oraz kąty między wiązaniami dla prostych cząsteczek [11].

Liczba obszarów o wysokiej gęstości elektronowej	Figura geometryczna	Kształt	Kąt między wiązaniami [o]
2	linia		180
3	trójkąt		120
4	tetraedr		109,5
5	bipiramida trygonalna		120 i 90
6	oktaedr		90

O kształcie cząsteczki decyduje również liczba niewiążących par elektronowych. Ponieważ oddziaływanie z niewiążącą parą elektronową jest silniejsze, kąty pomiędzy wiązaniami sąsiadującymi z wolną parą elektronową ulegają zmniejszeniu. W przypadku sąsiadujących kilku par niewiążących efekt ten ulega zwiększeniu. Najczęściej spotykane kształty przedstawiono w tabeli nr 2.

Tabela nr 2. Kształty i kąty cząsteczek z uwzględnieniem wolnych par elektronowych [11].

Liczba obszarów o wysokiej gęstości elektronowej	Ilość		Rozmieszczenie par elektronowych (przykłady)	Przewidywany kształt cząsteczki lub jonu (kąt między wiązaniami)
	wiązań	wolnych par elektronowych
2	2	0	CO2, BeCl2	liniowy (180o)
3	3	0	SO3, NO3–, BF3	trójkąt płaski (120o)
3	2	1	SO2, O3	cząsteczka kątowa (<120o)
4	4	0	CH4, H2SO4, ClO4−, NH4+	tetraedr (109,5o)
4	3	1	H3O+, NH3, PH3	piramida trygonalna (<109,5o)
4	2	2	H2O, OF2, H2S	kątowy (<109,5o – mniejszy niż w przypadku jednej pary niewiążącej)
5	5	0	PF5	bipiramida trygonalna (120o i 90o)
5	4	1	SF4	nieregularny tetraedr (<120o i <90o)
5	3	2	ClF3, BrF3	kształt litery T (<120o i <90o)
5	2	3	XeF2, I3−	liniowy (180o)
6	6	0	SF6	oktaedr (90o)
6	5	1	ClF5, BrF5	piramida kwadratowa (<90o)
6	4	2	XeF4	kwadrat płaski (90o)

Poniżej przedstawiono kilka przykładów, pozwalających w prosty sposób określić kształt cząsteczki (jonu) oraz przybliżony kąt między wiązaniami.

A) Cząsteczka HCOOH

1. Atomem centralny w cząsteczce jest atom węgla (C).
2. Wzór elektronowy:
3. Liczba obszarów o wysokiej gęstości elektronowej: 3
4. Cząsteczka opisana jest na trójkącie równobocznym, kąt między wiązaniami: 120^o
5. Ze względu na brak niewiążących par elektronowych na atomie centralnym, cząsteczka HCOOH może być opisana jako trójkąt równoboczny.
6. Jeśli uwzględnimy obecność wiązania wielokrotnego i związany z nim większy efekt odpychania, możemy stwierdzić, że kąt między wiązaniami jest inny niż 120^o, a cząsteczka nie jest idealnym trójkątem równobocznym.

B) Jon HCOO^–

1. Atomem centralny w cząsteczce jest atom węgla (C).
2. Wzór elektronowy:
3. Liczba obszarów o wysokiej gęstości elektronowej: 3 – kształt jonu opisany na trójkącie równobocznym.
4. W jonie występuje delokalizacja wiązania π:
5. Jeśli nie uwzględnimy większego odpychania związanego z obecnością wiązania π jon HCOO^– można opisać jako trójkąt równoboczny (kąt między wiązaniami: 120^o).
6. Jeśli uwzględnimy obecność zdelokalizowanego wiązania π, możemy stwierdzić, że kąt między wiązaniami jest inny niż 120^o, a jon ma inny kształt niż opisana powyżej cząsteczka HCOOH.

C) Cząsteczka XeF₄

1. Atomem centralny w cząsteczce jest atom ksenonu (Xe).
2. Wzór elektronowy (Uwaga, w przypadku tej cząsteczki nie obowiązuje reguła oktetu):
3. Liczba obszarów o wysokiej gęstości elektronowej: 6 – cząsteczka opisana na oktaedrze (kąty między wiązaniami: 90^o).
4. Wzór elektronowy wskazuje na obecność dwóch niewiążących par elektronowych na atomie centralnym. Odczytany z tabeli 2 kształt cząsteczki: kwadrat płaski.
5. Niewiążące pary elektronowe rozmieszczone są symetrycznie. Z tego powodu ich obecność nie ma wpływu na kąt między wiązaniami.

D) Jon I₃^–

1. Atomem centralny w cząsteczce jest atom jodu (I).
2. Wzór elektronowy (Uwaga, w przypadku tej cząsteczki nie obowiązuje reguła oktetu):
3. Liczba obszarów o wysokiej gęstości elektronowej: 5 – jon opisany na bipiramidzie trygonalnej (kąty między wiązaniami: 90^o i 120^o).
4. Wzór elektronowy wskazuje na obecność trzech niewiążących par elektronowych na atomie centralnym. Odczytany z tabeli 2 kształt: cząsteczka liniowa.
5. Podobnie jak w cząsteczce XeF₄ niewiążące pary elektronowe rozmieszczone są symetrycznie. Z tego powodu ich obecność nie ma wpływu na kąt między wiązaniami.

E) Cząsteczka NH₃

1. Atomem centralny w cząsteczce jest atom azotu (N).
2. Wzór elektronowy:
3. Liczba obszarów o wysokiej gęstości elektronowej: 4 – cząsteczka opisana na tetraedrze (kąty między wiązaniami: 109,5^o).
4. Wzór elektronowy wskazuje na obecność jednej niewiążącej pary elektronowej na atomie centralnym. Odczytany z tabeli 2 kształt cząsteczki: piramida trygonalna.
5. Obecność niewiążącej pary elektronowej na atomie centralnym powoduje zmniejszenie kąta między wiązaniami i deformację tetraedru (kąty ~ 107^o).

Podsumowanie

W ujęciu szkolnym teoria VSEPR opiera się o trzy proste założenia, wzory elektronowe i tabele kształtów cząsteczek. Zrozumienie teorii i umiejętność przewidywania kształtów cząsteczek oraz kątów między wiązaniami nie powinna nastręczać uczniom szkół ponadgimnazjalnych większych trudności. Na tej podstawie uczniowie mogą wnioskować o polarności cząsteczki, rodzajach oddziaływań międzycząsteczkowych i właściwościach fizyczny substancji.

Należy jednak pamiętać, że przedstawione ujęcie jest znacznym uproszczeniem. Odpychanie pomiędzy obszarami o wysokiej gęstości elektronowej może być omyłkowo utożsamiane jedynie z oddziaływaniem elektrostatycznym. W tym wypadku bardziej dociekliwi uczniowie mogą zapytać, dlaczego pary elektronowe odpychają się wzajemnie, a elektrony będące w parze, posiadające przecież taki sam ładunek, nie. Fakt ten może być wytłumaczony na podstawie zakazu Pauliego i spinów elektronów. Również z tego powodu traktowanie wiązań wielokrotnych, jako jednego obszaru o jednolitej gęstości elektronowej jest daleko idącym uproszczeniem. Czytelników zainteresowanych tymi problemami odsyłamy do bardziej szczegółowej literatury [8,9].

Literatura

[1] Rozporządzenie Ministra Edukacji Narodowej z dnia 23 grudnia 2008 r. w sprawie podstawy programowej wychowania przedszkolnego oraz kształcenia ogólnego w poszczególnych typach szkół Dzienniku Ustaw z dnia 15 stycznia 2009 r. Nr 4, poz. 17.
[2] M. M. Poźniczek, Zofia Kluz, Wybieram Chemię, ZamKor, Kraków 2008.
[3] R. Hass, A. Mrzigod, J. Mrzigod, W. Sułkowski, Chemia, Nowa Era, Gdańsk 2008.
[4] A. Czerwiński, A. Czerwińska, M. Kamińska, Chemia, WSiP, Warszawa 2004.
[5] B. Kałuża, F. Kamińska, Chemia ogólna i nieorganiczna, Wydawnictwo Edukacyjne Zofii Dobkowskiej, Warszawa 2003.
[6] K. M. Pazdro, W. Danikiewicz, Chemia, Oficyna Edukacyjna Krzysztof Pazdro, Warszawa 2009.
[7] N. V. Sidgwick, H. M. Powell, Stereochemical Types and Valency Groups, Proc. Roy. Soc. A, 176, 153-180 (1940).
[8] R. Gillespie, J. Chem. Educ. 81, 298, 2004.
[9] R. Gillespie, I. Hartgittai, The VSEPR Model of Molecular Geometry, Allyn and Bacon: Boston 1991.
[10] L. Jones, P. Atkins, Chemia ogólna cząsteczki, materia, reakcje. PWN, Warszawa 2006.
[11] J. Green, S. Damji, Chemistry 3^rd ed., IBID Press 2007.

Tekst opublikowany w czasopiśmie „Niedziałki” w 2012 roku. Opublikowano za zgodą redakcji czasopisma. Do napisania artykułu skłoniło mnie zadanie maturalne z 2011 roku, które znacznie utrudniło życie wielu maturzystom.

Paweł Bernard Niedziałki 1/2012, s.10-16

Wstęp

Egzamin maturalny z chemii na poziomie rozszerzonym w roku 2010/2011 nie należał do najłatwiejszych, a dodatkowo wzbudził sporo kontrowersji. Oto jedno z pytań, które sprawiło wiele kłopotów [1]:

Zadanie 14. (4 pkt) Poniżej przedstawiony jest schemat reakcji: MnO42- + H+ → MnO4− + MnO2 + H2O a) Napisz w formie jonowej z uwzględnieniem liczby oddawanych lub pobieranych elektronów (zapis jonowo-elektronowy) równania procesów redukcji i utleniania zachodzących podczas tej przemiany. Równanie reakcji redukcji: …………………………………………………………………………….. Równanie reakcji utleniania: ………………………………………………………………………….. b) Dobierz i uzupełnij współczynniki stechiometryczne w poniższym schemacie. ………. MnO42- + ………. H+ → ………. MnO4− + ………. MnO2 + ………. H2O c) Napisz, jakie funkcje pełnią jony MnO42− w tej reakcji.

W zadaniu uczniowie mieli za zadanie uzgodnić podane równanie reakcji w oparciu o zapisane pełne równania redukcji i utleniania. Ta metoda uzgadniania równań REDOX to tak zwana metoda równań połówkowych. Problem stanowi fakt, iż metoda ta nie jest wyszczególniona w obowiązującej podstawie programowej z chemii [2,3]. Z tego powodu praktycznie w żadnym polskim podręczniku do chemii na poziomie szkoły ponadgimnazjalnej metoda ta nie jest omawiana. Tradycyjnie uzgadnianie równań reakcji utleniania-redukcji opierane jest o bilans elektronowy nazywany równaniami cząstkowymi (często mylonymi z równaniami połówkowymi). Czym zatem różnią się te dwie metody?

Uzgodnienie w oparciu o bilans elektronowy

Uzgodnijmy podane w zadaniu równanie reakcji metodą równań cząstkowych.

1. Należy przypisać pierwiastkom stopnie utlenienia i znaleźć atomy, które ulegają utlenieniu bądź redukcji. W tym przypadku ww. zadania maturalnego zarówno utlenieniu jak i redukcji uległ mangan.

2. Zapisujemy schemat procesów utlenienia i redukcji w oparciu o atomy, które wzięły udział w każdym z tych procesów wraz z podaniem liczby przyjmowanych lub oddawanych elektronów. Liczba przyjętych i oddanych elektronów musi być równa w obu procesach, w tym celu dobierany jest tzw. „mnożnik”.

			Mnożnik
VI	red	IV
Mn + 2e–	→	Mn	1
VI	utl	VII
Mn	→	Mn + 1e–	2(1)

3. Wyznaczony mnożnik stanowi o liczbie atomów każdego typu. Na tej podstawie uczeń jest w stanie zapisać podane równanie reakcji w formie:

3MnO₄^2- + H⁺ → 2MnO₄⁻ + MnO₂ + H₂O

4. Ponieważ bilans elektronowy został uzgodniony dalsze uzgodnienie równia przeprowadza się w sposób klasyczny.

Metoda ta prowadzi do poprawnego rozwiązania zadania, jednak przedstawione równania cząstkowe nie są pełnymi równaniami reakcji utleniania i redukcji. Z tego powodu rozwiązanie to nie było punktowane.

Uzgodnienie w oparciu o równania połówkowe (równania jonowo-elektronowe)

Jak można wnioskować na postawie samej nazwy, równania połówkowe po zsumowaniu powinny stworzyć pełne równanie analizowanej reakcji chemicznej. Zatem zadanie to mogło być rozwiązane w następujących etapach:

1. Podobnie jak w metodzie bilansu elektronowego należy zacząć od przypisana pierwiastkom stopni utlenienia i znaleźć pierwiastki, które ulegają utlenieniu bądź redukcji. W tym przypadku do opisu procesów zapisujemy nie tylko atomy, których stopień utlenienia uległ zmianie, ale całe indywidua (cząsteczki, jony lub atomy) które biorą udział w reakcji. Zacznijmy od równania, w którym zachodzi redukcja:

VI	red	IV
MnO42- + 2e–	→	MnO2

2. Równanie połówkowe należy uzgodnić. Nie jest to jednak możliwe wprost, ze względu na różną liczbę atomów tlenu. W takim wypadku po stronie równania, w której występuje deficyt atomów tlenu dopisuje się odpowiednią liczbę cząsteczek wody:

VI	red	IV
MnO42- + 2e–	→	MnO2 + 2H2O

3. Dopisanie cząsteczek wody spowodowało deficyt atomów wodoru po stronie substratów. Deficyt ten uzupełniamy dopisując odpowiednią liczbę kationów wodoru:

VI	red	IV
MnO42- + 2e– + 4H+	→	MnO2 + 2H2O

4. W ten sposób równanie redukcji zostało uzgodnione. Kolejnym etapem jest uzgodnienie równania utleniania:

VI	utl	VII
MnO42-	→	MnO4− + e–

5. W tym przypadku liczba atomów po stronie substratów i produktów jest równa. Należy jednak równanie utleniania podwoić, aby liczba oddanych elektronów była zgodna z liczbą elektronów przyjętych podczas procesu redukcji. Następnie sumujemy procesy:

(1x)	MnO42- + 2e– + 4H+	→	MnO2 + 2H2O
(2x)	2MnO42-	→	2MnO4− + 2e–
Sumujemy równana stronami
3MnO42- + 4H+		→	MnO2 + 2H2O + 2MnO4−

W ten sposób otrzymujemy w pełni uzgodnione równanie. Schemat postępowania, tzn. dopisanie odpowiedniej liczby cząsteczek wody i kationów wodoru jest uniwersalny i znajduje zastosowanie przy uzgadnianiu zarówno równań zapisanych w formie cząsteczkowej jak i jonowej.

W przypadku przedstawionego zadnia maturalnego obie metody prowadziły do tego samego wyniku, zatem narzucenie formy rozwiązania zadania jest mocno kontrowersyjne. Dodatkowo układ graficzny zadania tzn. jedna pusta linia na wpisanie równania redukcji mogła być myląca i z pewnością utrudniała zapis rozwiązania.

Czy zatem stosowanie równań połówkowych jest potrzebne?

Osoba układająca pytanie mogła wymusić sposób rozwiązania zadania inaczej je formując. W treści zadania zamiast podawać pełny schemat mogła zapisać jedynie jego fragment:

MnO₄^2- → MnO₄⁻ + MnO_2­

Oczywiście podniosłoby to poziom trudności zadania, ale rozwiązanie tego przykładu w oparciu o bilans elektronowy nie byłoby możliwe.

Równania połówkowe znajdują często zastosowanie, gdy nie jest znane całe równanie reakcji, a jego zapisy jest opary o obserwacje.

Przykład 1 – klasyczny probierz trzeźwości

Wykrywanie alkoholu w wydychanym powietrzu było dawniej przeprowadzane przez tak zwane „dmuchanie w balonik”. Powietrze z balonika było przepuszczane nad pomarańczowym dichromianem(VI). Zmiana zabarwienia na zieloną związana była z redukcją dichromianu(VI) do związku chromu(III) i jednoczesnym utlenieniem alkoholu do kwasu karboksylowego. Równanie to można zapisać i uzgodnić w oparciu o równania połówkowe:

VI	red	III
Cr2O72–	→	2Cr3+
-III – I	utl	-III III
CH3CH2OH	→	CH3COOH

Uzgadnianie równania redukcji krok po kroku:

	VI	red	III
1	Cr2O72– + 6e–	→	2Cr3+
2	Cr2O72– + 6e–	→	2Cr3+ + 7H2O
3	Cr2O72– + 6e– + 14H+	→	2Cr3+ + 7H2O

Uzgadnianie równania utleniania krok po kroku:

	-III – I	utl	-III III
1	CH3CH2OH	→	CH3COOH + 4e–
2	CH3CH2OH + H2O	→	CH3COOH + 4e–
3	CH3CH2OH + H2O	→	CH3COOH + 4e– + 4H+

Sumaryczne równanie:

Mnożnik
(2x)	2Cr2O72– + 12e– + 28H+	→	2Cr3+ + 14H2O
(3x)	3CH3CH2OH + 3H2O	→	3CH3COOH + 12e– + 12H+
Sumujemy równana stronami
2Cr2O72– + 16H+ + 3CH3CH2OH		→	2Cr3+ + 11H2O + 3CH3COOH

Przykład 2 – redukcja manganianu(VII)

Fioletowy jon manganianowy(VII) uległ reakcji z siarczanem(IV). W wyniku reakcji powstał bezbarwny roztwór:

VII	red	II
MnO4–	→	Mn2+
IV	utl	VI
SO32–	→	SO42–

Uzgodnienie równania redukcji krok po kroku:

	VII	red	II
1	MnO4–	→	Mn2+
2	MnO4– + 5e–	→	Mn2+ + 4H2O
3	MnO4– + 5e– + 8H+	→	Mn2+ + 4H2O

Uzgodnienie równania utleniania krok po kroku:

	IV	utl	VI
1	SO32–	→	SO42– + 2e–
2	SO32– + H2O	→	SO42– + 2e–
3	SO32– + H2O	→	SO42– + 2e– + 2H+

Sumaryczne równanie:

Mnożnik
(2x)	2MnO4– + 10e– + 16H+	→	2Mn2+ + 8H2O
(5x)	5SO32– + 5H2O	→	5SO42– + 10e– + 10H+
Sumujemy równana stronami
2MnO4– + 6H+ + 5SO32–		→	2Mn2+ + 3H2O + 5SO42–

Na podstawie zapisanego równania widać, że reakcja zaszła w środowisku kwasowym. Do uzgadniania reakcji biegnących w środowisku zasadowym należy zastosować jedną z alternatywnych metod[4]:

Przykład 3 – redukcja manganianu(VII) w środowisku zasadowym

Redukcja:

	VII	red	VI
1	MnO4– + e–	→	MnO42-

Utlenianie:

	IV		utl	VI
1	SO32–		→	SO42– + 2e–
2	SO32– + 2OH–		→	SO42– + 2e–			Zamiast cząsteczki wody dopisujemy jony OH–­ (dwa jony na każdy brakujący atom tlenu)
3	SO32– + 2OH–		→	SO42– + 2e– + H2O			Po drugiej stronie równania dopisujemy cząsteczki wody tak, aby zbilansować równanie (jedna cząsteczka na dwa jony OH–­)

Mnożnik
(2x)	2MnO4– + 2e–	→	2MnO42-
(1x)	SO32– + 2OH–	→	SO42– + 2e– + H2O

Sumujemy równana stronami
2MnO4– + SO32– + 2OH–	→	2MnO42- + SO42– + H2O

Co jednak zrobić, gdy środowisko reakcji nie jest zdefiniowane? W taki przypadku możemy zastosować ogólną metodę (przedstawioną w przykładzie 1 i 2):

Redukcja:

	VII	red	VI
1	MnO4– + e–	→	MnO42-

Utlenianie:

	IV	utl	VI
1	SO32–	→	SO42– + 2e–
2	SO32– + H2O	→	SO42– + 2e–
3	SO32– + H2O	→	SO42– + 2e– + 2H+

Sumaryczne równanie:

Mnożnik
(2x)	2MnO4– + 2e–	→	2MnO42-
(1x)	SO32– + H2O	→	SO42– + 2e– + 2H+
Sumujemy równana stronami
2MnO4– + SO32– + H2O		→	2MnO42- + SO42– + 2H+

Zapis równań tą metodą może prowadzić do mylnego wniosku, że reakcja zaszła w środowisku obojętnym. Jednak, bardziej ostrożnie sformułowany wniosek, że pH w trakcie reakcji maleje, jest poprawny. Jeśli na tym etapie zostanie podana informacja, że początkowo pH roztworu było większe niż 7, równanie to można uzupełnić przez zalkalizowanie substratów. Osiągnąć to można stosując prosty zabieg techniczny – zsumowanie równania z równaniem autodysocjacji wody.

2MnO4– + SO32– + H2O	→	2MnO42- + SO42– + 2H+
2H+ + 2OH–		2H2O
Sumaryczne równanie:
2MnO4– + SO32– + 2OH–	→	2MnO42- + SO42– + H2O

Ostatecznie obydwie metody dają ten sam rezultat.

Podsumowanie

Równania połówkowe stanowią proste narzędzie pozwalające nie tylko dobrać współczynnik stechiometryczne do równań utleniania-redukcji, ale również uzupełnić równania o niektóre substraty lub produkty i na tej podstawie wnioskować o zmianie odczynu towarzyszącemu reakcji. Przedstawiona metoda uzgadniania równań połówkowych wydaje się nie być trudniejsza od metody bilansu elektronowego. Należy jednak podkreślić, że w przypadku gdy dysponujemy pełnym zapisem schematu reakcji, stosowanie tej metody nie niesie ze sobą korzyści, a może być uznane za dość pracochłonne. Niemiej jednak, mając na uwadze zbliżający się egzamin maturalny, być może warto poświęcić chwilę czasu na lekcji powtórzeniowej na omówienie tej metody, przedyskutowanie jej zalet i rozwiązanie poniższego zadania.

Zadanie

Poniżej przedstawiono zestaw schematów procesów utleniania i redukcji. Połącz procesy w pary i metodą równań połówkowych zapisz i uzgodnij odpowiednie równania reakcji. Uwzględnij wszystkie możliwe kombinacje (UWAGA: rozstrzygnięcie problemu, czy dany proces może zajść w rzeczywistości nie jest przedmiotem rozważań).

1. I. Co³⁺ → Co²⁺
2. II. PbO₂ → Pb²⁺
3. III. ClO₃^– → Cl^–
4. IV. Sn²⁺ → Sn⁴⁺
5. V. NO₂ → NO₃^–

Literatura

1. Egzamin maturalny z chemii, poziom rozszerzony, maj 2011 s. 8

2. Rozporządzenie Ministra Edukacji Narodowej z dnia 23 grudnia 2008 r. w sprawie podstawy programowej wychowania przedszkolnego oraz kształcenia ogólnego w poszczególnych typach szkół Dzienniku Ustaw z dnia 15 stycznia 2009 r. Nr 4, poz. 17

3. Podstawa programowa z komentarzami, tom 5. Edukacja przyrodnicza w szkole podstawowej, gimnazjum i liceum. Załącznik do rozporządzenia Ministra Edukacji Narodowej z 23 grudnia 2008 roku w sprawie podstawy programowej wychowania przedszkolnego oraz kształcenia ogólnego w poszczególnych typach szkół z komentarzem.

4. L. Jones, P. Atkins, Chemia ogólna. Cząsteczki, materia, reakcje. s.387, PWN, Warszawa 2006

---

(1) Zapis oddawanych elektronów w procesie utleniania po stronie substratów ze znakiem ‘-‘ stanowi zapis alternatywny traktowany równorzędnie z podanym.